重复数据删除综述(4):可靠性问题、纠删码技术
在存储系统中,单纯地通过增加完全副本冗余来提高系统的可靠性并不能保证在错误出现时,数据仍具有持久性和可靠性。因此一些研究者提出利用纠删码技术对数据做一定的冗余来增加系统的可靠性。纠删码技术是指将要存储的数据切分为k个部分,然后通过编码算法变换为n(n>k)个部分,其中任意k′(k′≥k)个部分可以用来恢复原始数据。当k’ = k时,称编码算法具有最大距离分割性质(maximum distance separable,简称MDS).
纠删码主要分为4大类:Reed Solomon Codes, Parity Array Codes,Parity-check Codes和LDPC(low density parity check)Codes。其中,Reed Solomon Codes是基于有限域运算的,后三者主要是基于XOR运算。每种纠删码(erasure codes)都有其各自的优缺点:
1) Reed Solomon码:
i.MDS码,具有最优的存储利用率;
ii.容错能力k′可以为任意数;
iii.数据出度总是大于k′,从而有较高的更新(update)复杂度;
iv.复杂的代数运算。
2) Parity Array码:主要是通过单元的二维空间几何分布构成的,适用于RAID系统。
3) Parity-check码:从奇偶校验码发展而来的多维码,特点是简单且完全基于XOR运算,容易实现,且更新(update)和解码(decode)等操作都具有较好的局部性,其缺点是非MDS,主要适合于大规模存储系统。
4) LDPC码:基于Tanner图发展起来的一维码,其构造主要是基于图论和蒙特卡洛法。其优点是可以完全用XOR运算实现,并且其存储利用率接近MDS。其解码算法主要是采用迭代方法实现,可以达到很高的容错能力,但是容错能力越高,其构造越不规则,从而导致不易实现。
当前在重复数据删除系统中应用纠删码技术来提高系统可靠性的研究还较为简单,仅局限于Reed Solomon纠删码。因此,如何引入其他纠删码技术提高系统可靠性,将有待进一步的研究。
经典文献
uImplementation and performanceevaluation of fuzzy file block matching
Han B, Keleher P.. In: Proc. of the 2007 USENIXAnnual Technical Conf. (USENIX 2007). Berkeley: USENIX Association, 2007.199−204.
站内头条
-
NetApp 与 Google Cloud 合作,简化在云中扩展高性能工作负载的过程
2025-04-12 -
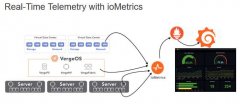
VergeIO推出 ioMetrics 监控平台,实现基础设施的深度可见性
2025-04-12 -
遵循 Zero Trust 的不可变备份存储是抵御勒索软件的最佳方法
2025-04-12 -
PNY 发布 PRO Elite 高耐用性 microSD 闪存卡,容量高达 512GB
2025-04-11 -
DDN 与 Google Cloud 合作,推进AI计划
2025-04-11